Ok so I am gonna do 1 hour to warm up.
Powers and roots
First thing I didn’t remember is that any non 0 number to the power of 0 = 1. Noted.
Odd exponent preserves the sign of the base. If even, always positive result. (as long as the base different of 0).
Suggests to memorize some basic powers:

Hmm… won’t do now unless needed later
Trick for squaring numbers ending in 5. This I didn’t know but anyway I learned just in case. Basically any number ending in 5 its square can be easily calculated by taking nums in front of the 5 , multiplying it by itself+1 and then putting 25 after that. So for ecample 235^2 is (23*24) = 552 and put 25 after hence 55225.
Exponent laws
If same base product with diff exp, u can add. If divide u can substract. If power to a power we can multiply the exponents. This I remember from high school.
Most I know but something I have not used much and didn’t remember is the combining bases law that says x^n * y^n = (xy)^n. So for example 2^3 * 7^3 = 14^3. Not sure when this will be handy but interesting. Actually it makes sense… cause if I deconstruct an integer into its components such as 30 (3*5*2)… then It’s clear to see that 30^2 = 3^2 + 5^2 + 2^2.
Some questions basically ask “what is the units digit of N^big exponent” such as 53^35. Important to know that we need to only do the first step of the multiplication each time, to find the pattern that repeats… then it’s easy to know the units digit of any exponent of 53. CAREFUL … not to forget the N^1 digit in the cycle. I made that mistake in my calculations and gave me the wrong result even doing the method right. For sure I will need a good night sleep before the GMAT or these “stupid
mistakes” are gonna get me in trouble.
Square Roots
square(n) is a number (positive) than when square gives n.
square(0) = 0.
Again suggest to memorize some basics:

These I won’t memorize for the moment but hope to organically do eventually .
square(x^2) = absolutevalue(8)
Also as we know that exponentiating a number between 0 and 1 makes it smaller… the square root of x being between 0 and 1 is greater than x. And the opposite happens when x is greater than 1.
Other Roots
Odd roots. We can find the odd root of a negative number. The odd root of a negative number will be negative. The odd root of a positive number will be positive
Even roots: We cannot find the even root of a negative number. Even root of a positive numebr will always be positive.
All roots have at most 1 value.
Hmm I can see some trouble coming from not having enough practice with exponents and memorizing. Hope it doesn’t become a problem.
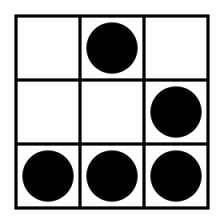
This question:
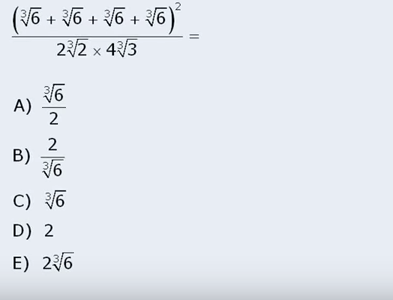
I solved in 2min correctly. Clearly Iam quite rusty :S. Might need to do some roots manipulation to speed things up.
Equations and Powers
Rule: if b^x = b^y then x = y (except when base = 0 or 1)
This again seems easy.
Fixing the denominator
If answer has a root in denominator one can take it out by multiplying top and bottom by that root. 🙂 Important to keep this in mind!
ALARM misbehaved – stopped and forgot to turn on again. I am not sure how much time has passed… maybe 1:45 min? Put 2 hours on clock now.
To fix something like below you can use the conjugate. Damn haha this vaguely came to my mind when reading the question. I remember doing this in high school.

Just be careful to know that (a+b)(a-b) = a^2 – b^2 (that – sign is important).
Ok this question below totally got me:
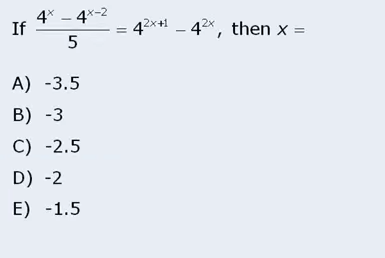
No idea how to solve. Ok after 15 minutes thinking I suddently decided to deconstruct the exponents… and then it made sense… took a long long time, but go it. Hmm… not sure why I didn’t try it before. Mainly I think I am not confident enough doing operations with exponents. Definitely need to practice.
Now in the video this is solved by factoring and exponential equation. Although I am not 100% confident with the system, just knowing that I can expect this kind of operations is already very helpful. Let’s see how I react next time I face a similar problem.
This question
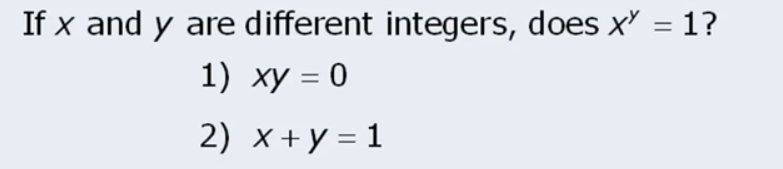
I solved right but took me 5 min, so total failure.
I’m gonna really focus on what went wrong and how to improve.
Ok I think I got it… so the process is to say “I am gonna check different values of x and y that satisfy condition 1. I am then going to check if they satisfy the question target”. And do the same with 2. I think with this method Ill be able to unblock in situations like this question.
Damn damn damn this question also got me :S 🙁
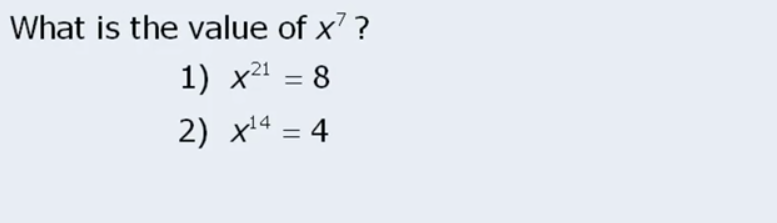
I am not sure at this pace 🙁 how well Im gonna do… I guess as long as I don’t repeat same mistakes 🙁
Here first I failed to realize that x^21 is (x^7)^3. I had done (x^7)(x^7)(x^7) but just didn’t really see it being the above. Then even after knowing that, there are more hard stuff… now that we know (x^7)^3 = 2^3 the smart thing is to realize that x^7 will be 2, and only 2 because exponent is odd. If it was even then -2 will also work.
On the expression below, we see that x^7 has to equal 2, but the thing is… it could also be -2 and give the same 4 result once squared hence it is not sufficient. DAMN DAMN DAMN I should be sharper. I get all this and know it, but just don’t do it when I am answering the question.
Check this question:
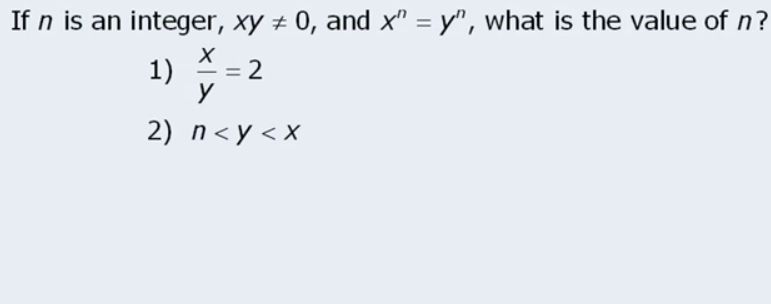
Again didn’t know how to solve :(. Thing is, I did the table thing that make me understand that statement 1 is sufficient, but statement 2 I was not clear. Moreover statement 1 I was not 100% sure I was fully right.
The issue is that this question really is complicated. First of all… x^n = y^n I never “re-wrote this”. If one re-writes it to (x/y)^n = 1 then things become a bit more manageable.
In this situation one needs to be smart enough to understand what are ALL cases in which that equation is met. This is not trivial. Well it turns out there are 3 cases. Case 1 is when x/y = 1 and n is ANY value. Case 2 is when x/y is -1 and n is ANY value, case 3 is when x and y are ANY value and n = 0. With this in mind we can go ahead evaluate.
First case tells us x/y = 2 hence already we know it can only be the other case where x and y can be any value and n = 0 hence sufficient. Statement 2 on its own however… tells us that y and x are not the same hence we know that to yield 1 will be impossible so case 1 is not. Then case yield -1 will be possible with something like 2 , -2 for intance… now, in that case N can be anything, so n surely can be any number less than -2 and still will hold hence we don’t know the value of N. that already means statement is insufficient. Case 3 if we analyze we see that n would be 0, and y and x could be any number… but still is NS because we know N can be many other numbers besides 0.
Learned that problems can indeed get super complex. Cases must be split, I must try to find ways to rearange given equations to make my lfie easier.
Ok I got 3 or 4 right in a row. Even some hard ones like this:
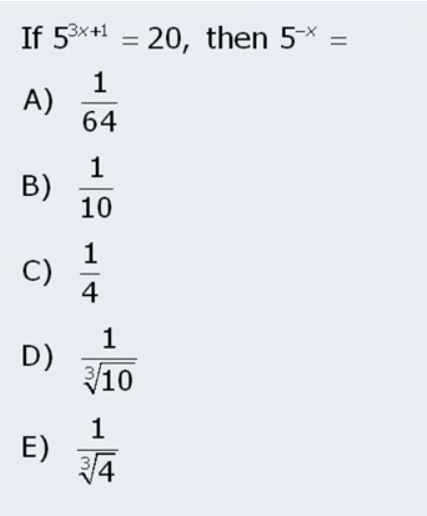
Good… maybe little by little the concepts really are starting to sink in, which is good.
Done with the powers and roots module! Let’s get into Algebra!
Starting all very basic. I have decent algebra basics :)! Again high school does help.
Alarm sounded. Gonna put 2 more hours. I am watching videos quite quickly as quite basic.
Ok so I just got absolutely owned by this:

Certainly I am not thinking straight.
Did it again and took me 1m 52 s to find an answer just by doing a simple substitution by 1 instead of trying to simplify the heck out of the equation.
Now in the video he actually simplifies… in order to be able to do it efficiently there is one thing I had not memorized that I need to memorize which is that (a+b)(a+b) = a^2 + 2ab + b^2 .I just need to be sharp enough to look at an equation and realize if that meets or not.
Question below is hard:

Thankfully I took right approach and decided to substitute values for x and y. Got right answer although in 2m 10s, because of making some silly mistakes when calculating
Next question also was interesting:
This one again I got right in 2min approx 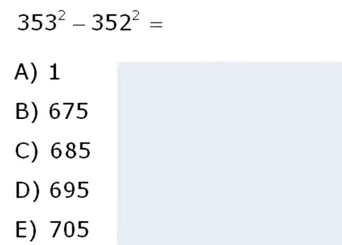 … at the beginning I didn’t know what to do… but then I realized the expression was equal to (352+1)^2 – 352^2 and by expanding that got to the answer.
… at the beginning I didn’t know what to do… but then I realized the expression was equal to (352+1)^2 – 352^2 and by expanding that got to the answer.
Actually there is a MUCH quicker way … that is realizing the numbers are a substraction of squares a^2 – b^2 hence we can know that they come from (a+b)(a-b). Which takes us to answer much quicker.
Equations
This is also simple. Went also through quadratic equations. Also sistems of linear equations. Hmm… interesting the “Elimination method” I just needed to refresh it a bit.
Systems of equations can have one solution, infinite or none (if x + y = 2 and x + y = 23 for example). If both equal, then infinite number of solutions.
Systems of 3 equation swith 3 unknowns. Follow similar process. Just convert into 2 by substitution and then solve.
Interesting… I don’t know why this is counterintuitive… but in an equation I can raise both sides to the power of 2 for instance and still meets the conditions. Well I guess it makes sense actually… because if a = b then a^2 must equal b^2 .
Extraneous roots
root(k)^2 = k for k bigger or equal to 0. Careful sometimes exponentiating etc to eliminate roots might give results that are not valid as when substituting u find u are dealing with a negative root.
Equation with absolute values
Here the important thing is to realize that if abs(x) = a then x can be x=a or x=-a . So we can do that whenever we encounter an equation with absolutesl.
Careful: When doing equations with absolute valeu there can again be extraneous roots. So need to check the answer on the original equation and see if it makes sense or not.
Check this question:
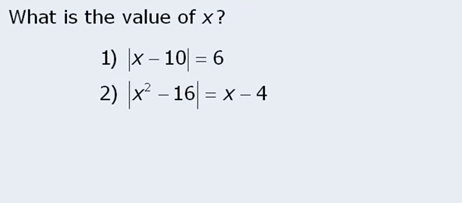
It’s a shame because I did the whole process well but made a little mistake in an addition hence I got confused :(. Need to be very careful when doing calculations. It gives me peace to know that the method I was using was right though. Honestly if I hadn’t studied this absolute value section I wouldn’t have been able to answer these kinds of questions.
Remember, all one needs to remember is that the equation can equal either a or – a and then make sure to double check your answers in original equation to see if any extraneous root is there.
STUPID MISTAKES – > Are happening much more often that I would want to. Hmm… I am thinking that still is early on my study so its normal… but I am also thinking it might have to do with the process I am using. I am doing a lot of calculations on my head and I think that’s causing it. So I will try write more on paper and see what happens.
Inequalities
Finally. 😀 I have trouble with these so looking forward to refresh this.
Rules:
- I can substract or add both sides … and it remains intact
- I can multiply or divide both sides by a positive number and it remains intact.
- I can multiply or divide both sides by a negative number but that will REVERSE the inequality
Nice …. so it’s actually like an equation pretty much.
If inequality has 3 parts then we can still do the operations above highlighted.
Try this question
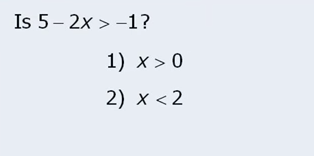
I solved properly in 38s. Nice.
Check this one:
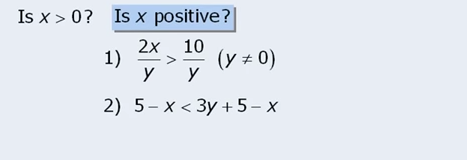
I solved in 3min 14s unfortunately, but I am happy I actually solved it. It was pretty damn hard.
I took correct path by understanding that there are 2 cases, y is positive or y is negative. Still I could have done it even better by just rearranging the inequalities in those 2 cases. What I did was a bit more convoluted.
Combining Inequalities
Rule 1 : Rewrite inequalities facing the same direction before trying to combine them .
Adding Inequalities
Remember sign has to face same direction.

Rule 2: Do not substract , divide or multiply inequalities. It doesn’t work.
Rule 3: You can add inequalities , it works.
Check this question:
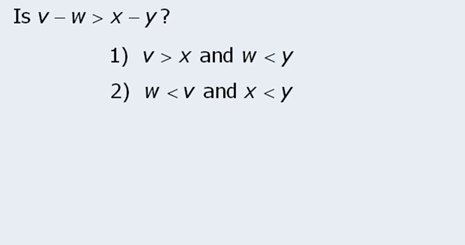
Im thrilled to announce that I got it right, although it took me 3min to get it right.
Process wasn’t flawless… but eventually it worked.
In the video solution he uses a much quicker method by adding the inequalities. I understand the concept… let’s see if in future questions I can use it though…
ALARM sounded so 2 hours passed. Ill take 10 min break and will resume after. Hmm… I shouldn’t go sleep after 2am though.
Inequalities and absolute values
Here the main rules
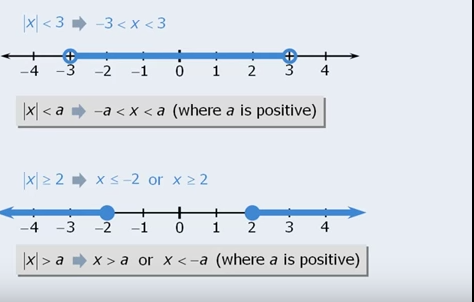
Hmm I have not memorized them but I understand the concept. So if a number is more than an absolute value x it means than X is closer to the center than that number. If a number is less than an absolute value X it means that abs(x) are all values further away from center starting on a.
if I have abs(x) < 5 then I need to complete adding engative number -5 < abs(x) < 5 and then remove abs so -5 < x < 5. Ok I think I got this memorized 😀
If abs(x) > 5 then I need to again do the same -5 > x > 5 however it can’t be both so it will be wither one or the other hence -5 > x OR x > 5.
Quadratic Inequalities (really? XD)
Ok basically one finds the solutions, which are the “0 points” where the funciton cuts the axis. If we found 2 solutions then we know we can divide the number line in 3 segments (left of first 0, between 0 , and right from right 0). So u just need to test a number in each region to know what sign is that range having and that’s all, you can then find the solution to the inequality.
Check this question:

Unfortunately again I made a very very stupid mistake. I am happy because I did the process right… but sad I made such a stupid mistake. Basically I found of course the breaking points 1 and3… but the thing is… when I substituted 2 into the equation to see the sign… I was convinced it was giving me positive… not sure why… I thought it was 2x instead of 4x … really weird . Anyway It’s a bit late maybe that is affecting.
The something technique
Ok so this is an interesting technique to solve equations. Having said that, I honestly prefer to substitute values, I find that’s pretty quick generally. In any case this technique is defintiely good to know.
Again pretty sad because I did the process well but got it wrong due to again a STUPID little error in my factoring. Seriously sad.
The coordinate plane
This is it:
Hmm this should be easy.
Just need to remember coordinates is (x,y)
Distances in the coordinate plane
To find distance just make a right triangle and with pythagoras theorem know the hypothenuse.
Graphing lines in coordinate plane
Easy. Just find where y is 0 and x is 0 connect.
Slope of a line
Go from one point to another, slope is the ratio of upwards movement by horizontal movement so increment of y / increment of x (Can be negative or positive slope). (a,b) (c,d) the slope is (b-d)(a-c).
Vertical line has undefined slope.
As magnitude of slope increases, line gets steeper.
x and y intercepts
Easy no need to explain.
Slope y intercept form
y = mx + b – This tells us already a lot. m is slope, b is the y intercept! Nice.
Graphs of quadratic equations
Just know poiints that are on parabola satisfy equation. Also points are symetric on an axis of symettry, so same distance from it.
Ok, so all this I knew.
DONE with this module! 😀 ! Now only some exercises remaining which I will do, and I can close this module. This was a 50+ video module. Did pretty quickly as a lot of the basic things I knew, and also I am using 2x speed on the videos.
Ok So I am gonna do 19 practice questions let’s see what I get.
So far got 11 right and 2 wrong… but I am a bit tired so better stop. The hardest ones I can do tomorrow.
Been a good day. Did quite a lot.