Statistics, counting and probability… the last 3 topics. Had a long day, managed to get quite a lot of verbal reasoning and sentence correction done in between meetings etc using prep4gmat app… really reccomend it. I wanna get now 4 hours of quant done. Tomorrow I think I am gonna have a FULL free day!!!! I am SO looking forward to it. If it does hapen then I will have so much time to push.
Common let’s do this!
Statistics
Average, arithmetic mean, mean
This is easy. Sum of n numbers divided by n. Influenced by outliers.
Median
This is basically the middle number on an odd list of arranged numbers from low to high, or the average of 2 middle ones if list is even.
The median is simply the point where 50% of the data is above and 50% of the data is below. It is also the point that minimizes the distance from it to any of the other points in the dataset. It is a statistic not influenced by outliers.
Mode
The number that occur most frequently in the set.
Rule 1: In this set 4,4,5,5,7 for example, the mode is 4 and 5. This is important to know.
Properties
Rule 1: If the numbers in a set are evenly spaced, then the mean and median of that set are equal. (Evenly spaced means difference between 2 adjacent numbers is same as any 2 adjacent numbers of the set). This also works for negative numbers too. We can not say though that if mean and median same, the numbers are evanly spaced. That doesn’t work.
Weighted averages
If you have 2 groups of numbers with same number of numbers in both, the average of the combined 2 groups is the same as the average of the averages of each group. If the groups don’t have equal numbers thought, then you need to “weight” each average. Actually when only 2 groups with same… at the end of the day you are wighting the average by 1/2 each, so it’s better to just learn the below.
Weighted average: (Group average1) (proportion) + (Group average 2) (proportion) …
3 cases come from the above that one needs to keep in mind. Imagine u have 2 populations A and B with averages a and b. Well if popA = popB then avg is (a+b)/2. If A > B then we know average will be closer to a than b and viceversa.
Measures of dispersion
These are ways to measure how much a group of values is “spread out”.
RANGE: Greatest number in the set – Smallest number in the set. (Limitation is that it only tells us about the extreme values in the set)
STANDARD DEVIATION: Measures the extent to which all data values deviate from the mean. In other words “Is the average distance the data values are away from the mean”.
To calculate the standard deviation we need to know the mean and the number of values.
Below you can see how it is calculated (not required for GMAT). Basically measure how far each value is from the mean, square to make all positive, take the average of those distances, and eliminate squaring by taking the root.
VARIANCE
This is the value right before we take the last root on the Standard Deviation to “reverse” the squares we did before. So effectively Variance is the standard deviation squared.
UNITS OF STANDARD DEVIATION
How many SD’s u are from the mean.
Consider this question:
Hmm… although took right approach, I made a mistake in thinking that if 2 numbers add to 30, then one of then must be greater or equal than 25 which is notright as I can have 15 15. In the future if ever I encounter such situation for example… a+b = 35, so what are possible values for a and b? One thing I can do is to divide by 2to see values close to each other… in this case 17 and 18. thats the closest they are gonna get… So by dividing by 2 I will make sure I know all cases.
More interesting properties.
If I have a set of numbers with mean M, and add K to each number, the new mean will be M+K and the standard deviation will be the same as it was before.
Consider this question:
Now, if you remember that in a set of even spaced numbers, the MEAN and the MEDIAN is the same, immediately you know answer is 0. I forgot the rule so had to calculate which gave me right answer but took 2,5 min which is not good.
May this be a lesson for the future. Know your properties.
Consider this question:
Now hmm the thing is, I used the weighted average approach which gave me the right value but its not the quickest. The other way to solve it that I missed would have been realizing that again… if I am given n of population and average, I can know the sum of the population. In this case I am given the total n and the total average hence I know the total sum. I am also given n and sum for 2 and 3 guys and I am asked to find the value of the remaining guy. So quickly one can see that I just need to do mean n + mean2 n2 + remaining guy = totalmean + ntotal
Which is a faster approach.
Consider this question:
Now in this question the main problem was that I forgot about the “Positive Integers” part. Everything else I did correctly, but by forgetting that key bit, I got the wrong answer. Again, hmm… when writing the integers as a, b etc… on my paper, I didn’t put any note regarding them having to be positive. So next time if a condition like that is given, I must NOTE it on my paper once transcribing the question otherwise this will happen.
Once you have to solve a question in less than 2 min, there are no stupid mistakes. Every mistake is a mistake that was caused by something… and those mistakes and the speed is what I guess differenciates an OK score from a great score.
D0ne with this section! 😀
I am 70% confident with this section. Will have to surely revise, but I need to revise Geometry etc more.
Counting
So here we are! In counting! This is a very interesting and fun section. If you remember on my first day I did a bit of it and tackled some interesting problems. I am looking forward to revise this again.
Listing and counting – Hm… many cases not fastest way but sometimes might be considered. Important if listing to do it in a systematic way. Counting tree.
Counting tree is a beautiful way to list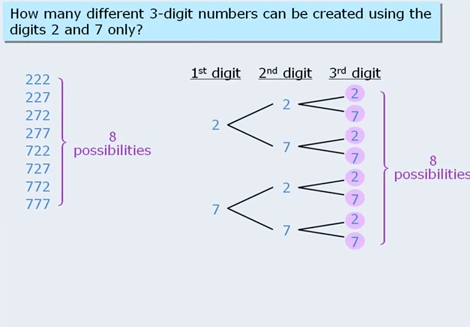
and also to understand structure.
Omg, one of the first problems is this one… later I found it is especially hard maybe even too hard for gmat.
How to list systemtically in such case is very important. I didn’t know how to do it.
Fundamental Counting Principle
This makes sense. Similar to “BOX” method I use.
Next video actually is the box method explained:
Hmm… important to be diligent when using the method.
Factorials
This we have done before.
If we have n unique objects, we can arrange them in n! ways.
The simple counting problems I am confident and can solve in 30 s or so, but yeah, complex ones take time.
Consider this question.
This one I solved in 1m 10s.
Restriction Rule: N of ways to follow restriction = N ways to ignore the restriction – N ways to break the restriction
I don’t think I will have to use the above though.
WRONG I do it seems.
Consider this question:
Now this question if you don’t use the above rule, it becomes pretty pretty hard, so I MUST learn that rule.
Now first of all if I wanted to follow normal method then how would I do it? Well I didn’t think of it but basically one needs to realize there are 3 cases… numbers with 1 seven, numbers with 2 and 1 number with 3.
Now that I think of it this could be a viable strategy too. There is only 1 num with 3 sevens. There is 9+8+9 numbers with 2 sevens as you can arrange the boxes as: (8*1*1) (1*1*9) (1*9*1) . And then there are 8*9 + 9*8 + 9*9 numbers with 1 seven. As you can arrange the boxes as (8*9*1) (8*1*9)(1*9*9). Note that in the places where 0 can be put , there are 9 digits that can go, in the places 7 is there, there are 1 choice only, and in the places where 0 can’t be there are 8 options only (1,2,3,4,5,6,8,9)
Now the other approach is to think… let me calcualte all numbers with 3 digits (9*10*10) = 900 and then lets substract all numbers that have NO 7’s… (8*9*9) = 648 hence the result = 252 = D
Hmm hard problem indeed.
TIP: In the future questions “at least” or “at most” indicate usually that the fastest way is to use the restriction rule.
Arranging letters where some are same.
To arrange letters NANNY for example… its important that we eliminate the effect of the 3 N’s by dividing by 3 factorial. Rule is below:
Combinations
Order of selected objects does not matter.
The important thing to remember again is that order does not matter.
Quick way to do combinations
Actually the method explained here, is what I actually do when I tackle a combination
Important combiantions property.
If we have 5 objects, and we have to see how many combinations are there if I chose 0,1,2,3,4,5 objects, there is a way one can calculate this easily.
You can see the method above.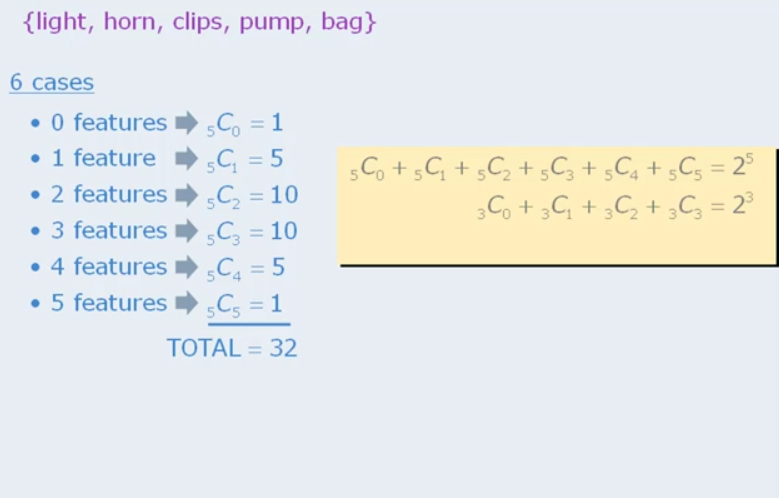 
Basically if we do all the way from nC0 to nCn the result is 2 to the power of n.
Another interesting property
Hard to visualize but basically taking 6 people and selecting 2 on comitee and its same as taking 6 people and selecting 4 of them not to be on the committee.
Selecting 1 person to be on comitee is same as selecting 6 people NOT to be on comitee.
The generalization of the formula is: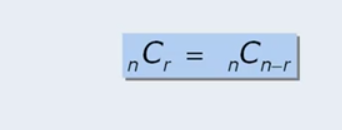
DONE :D!
Hence the current progress is as follows:
Only Probability is left! After that, I plan to do a bit of quick exploration on some videos regarding advanced strategies for quant section, and then probably its time to do a practice test using the OfficialBook see what happens. Then after that one I can correct mistakes and then probably take a proper practice test using the software? We will see! I wanna revise geometry, word problems and also every other topic briefly too … don’t wanna waste the tests unnecessarily.