Day 1 – Understanding the GMAT structure – Timings
First I want to understand the structure. Seems simple. So first I have 30 min to write an essay, I heard this is easy. Then I have 30 minutes to answer a new part called “Integrated Reasoning” which does not count for the 800 anyway. And then the proper stuff comes, 37 Quantitative (problems solving and data sufficiency questions) and 41 Verbal (reading comprehension, critical reasoning and sentence correction questions). Each of those sections is of 75 minutes which gives us 115 sec per quantitative question (so I should aim for 1:40 per answer max), and gives us 110 secs per verbal approx, so I should aim for 1:40 anyway there (although in this case time is harder to calculate as questions precede a text and mainly takes time to read the text.
Understood. So I need to crack those 2 75 min sections, ensuring I can answer every single question in 1:40 max. Ill aim for that. Will focus on math firstly. IMPORTANT to identify each question, what kind of question it is before even begin answering.
After 5 hours of study…
Ok, so I start to understand what the challenges are going to be.
I saw a video, and then on the first 20 secs of the second one I stopped. It took me 6 minutes to find the solution using the method learnt in video 1, and it was not pleasant and at 6 minutes would mean total failure. Although obviously I know I will do it much quicker with practice, the “brute force” method looks to rustic and too basic to be effective especially if bigger numbers come. This is what led me to start exploring methods on my own even before continuing the video. This exploration led to a 5 hour research into Combinations and Permutations, which it turns out I didn’t really need for this, and then also research into the fastest methods to factorize and find positive divisors.
Factorizing Quickly, finding positive divisors quickly
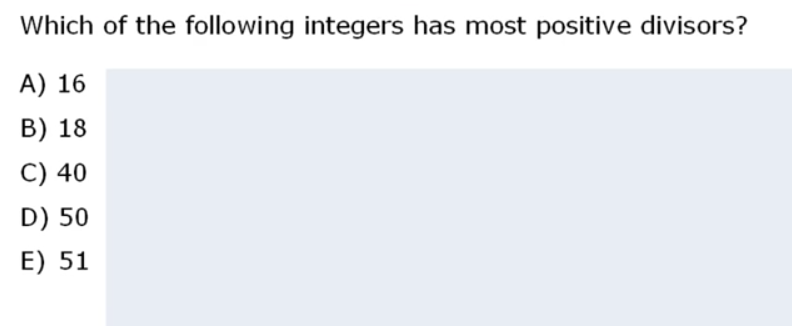
To understand the kind of challenges coming… Consider for instance this question which I think comes under “Properties of Integers” (which btw seems to be the most frequent subject appearing on the exams):
Now, the concept behind is pretty damn easy… but the thing is, can you get to a solution in less than 1:40 min? Good freaking luck if you are trying this for the first time. Now… I have realized that first, mental agility is going to be MASSIVELY important. This means I need to keep exercising and learn methods for each kind of question… gonna be tough, but I enjoy it.
How to find the positive divisors of a number quickly, the ultimate method:
It is very interesting because I had to do some research to find a method I felt comfortable with, which it turns out it is the method the same video series will teach in the future on Lesson 9. So the method I researched on my own seems the best. The key is here:

In case it is not clear, you just need to factorize the number as quickly as you can (this takes skill also)… which you do by saying… 14000 divided by (5.2) is 1400 (you note 5.2), divided by (5.2) is 140 ( you note 5.2.5.2) divided by 5.2 is 14 (you note 5.2.5.2.5.2) divided by (2.7) is 1 hence the result 5.2.5.2.5.2.2.7 or the same (5^3)*(2^4)*7 . Hence using formula above integers positive are 4*5*2 = 40.
As you can see, how quickly you factorize is very important and the more u can do in bulk the better. For me if I see a number like 14000, the smartest would be to take it down to 14 in one go, by realizing (10*10*10) is (5 ^3) * (2^3). And then its very easy to break 14 into pieces.
The pesky primes
Once factorizing I have realized that I get sometimes stuck if a prime appears… cause one tries to divide it but can’t. I must try to learn by heart the primes from 1 to 100 if I wanna speed things up, and also revise my basic tables of multiplication.
Now, hard memorization wouldn’t probably be cost effective… so what I am most probably going to do is reinforce my basic tables of multiplciation, which already will give me a good idea in helping to quickly determine if a number is part of any of those or not. I can anyway quickly discard 2,3,4,5 very quickly so I need to strengthen my 7,8,9 tables especially.

In conclusion
I feel I have learned how to find the postive integers of a number quickly very very well, and if a question comes up, I should be able to very easily and very quickly find the answer. I have used a randomizer to create the same kind of question and I am happy with the results. This topic is thus closed forever. It should be etched in my memory forever.
Some last quick notes on integer divisors
An important concept explained in video one was… that if an integer y is a divisor of an integer x, this means:
- That x/y yields 0 remainder
- That y is a divisor of x
- That y is a factor of x
- That x is a multiple of y
- That there is an integer k that exist such as x = yk
It is very important to understand that all that is the same, and to ingrain it in my mind.
Combinations and Permutations
I ended up exploring this usually “scary” topic by chance, while trying to find a method to quickly calculate the positive divisors of an integer. Although at the end it didn’t really take me anywhere, it was a GREAT way to organically getting introduced to both which I will definitely need in the future.
The knowledge of this topic I have acquired is about 70% out of 100%. I can answer most common questions now, but don’t fully fully understand the concept well enough to be 100% confident. This of course CANT be. I need to be 100% confident with everything.
Things I have understood:
The key to solving this problems is “Counting” , being these videos the best I have found so far. Things I have had to refresh and learn:
- Factorial of 0 is 1 …. 0! = 1
- Permutation is used for “arrangements” where the order matters
- Combinations is used for “selections” where the order doesn’t matter
- The best method found so far to solve problems is by drawing grid or “boxes” and thinking what can go in each.
- If a rearranging elements question comes up, and repepated elements are there, you can eliminate the effect of the n repeated by dividing by n! of each repeated element.
For example, how many ways I can rearrange MOOC into 3 letter words? (Order matters).
I make grid of 3… in first box I can put 4, on second 3 on thirf 2 hence 24 posibilities… however as O is repeated twice I need to divide by 2! hence final answer is 12 possibilities.
For a problem like below…
Again, if my understanding was 100% I’d be able to confidently apply the formulas directly and do it quickly. Unfortunately I am not yet there, however I can still get to the answer by using logic following the next reasoning:
I have 4 aces, and 48 reamining cards. I then draw the boxes, in this case 5 boxes as there are 5 positions to be filled. After this, I start filling… so on the first slot, any of the 4 aces can go so I put 4. On the second one of the remaining 3 aces can go so I put 3, on the next one one of the remaining 2 can go so I put 2 hence so far (4,3,2,_,_). Now, careful… because in this case ORDER doesn’t matter, we are not arranging, we are just selecting. For 3 slots, the number of different arrangements for 3 cards is 3!, hence I will need to divide (4*3*2) by 3!. Then for the remaining 2 slots, I can chose 48 cards for the first one and 47 for the second one… CAREFUL, ORDER doesn’t matter, we are not arranging we are selecting… so for those 2 slots, there are 2! arrangements for the 2 selected cards, hence we will have to divide (47*48) by 2! . Hence final result is ((4*3*2) * (47*28)) / (3! * 2!) = 4512
This is the same as saying… I need to select 3 aces out of 4, and 2 cards out of 48. So you can use the notation for combination (3 over 4) * (2 over 48). But I am not there yet.
The spirit
The main thing I want to say after this first day… is that I have ended the study craving for more, wanting to do many mor hours. I am thorougly enjoying this, which was the purpose on the first place. And this is the key. This is what matters. If I keep enjoying if I keep going deeper, I am confident I am gonna be able to have a solid performance.




Divisibility rules will also be helpful to identify primes (maybe even more than multiplication tales).
http://www.basic-mathematics.com/divisibility-rules.html